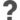@cstross @mjd @gregeganSF - Egan's original post says that the rakalis "figured out" something, and that may be true. Birds and mammals have culture, where behaviors are passed from one individual to another by learning. But the garter snakes probably didn't "learn to" do what they're doing. It's almost as quick to say "evolved to", and that's probably what happened.
J
johncarlosbaez@mathstodon.xyz
@johncarlosbaez@mathstodon.xyz
A forum for discussing and organizing recreational softball and baseball games and leagues in the greater Halifax area.
Posts
-
The rakali (Hydromys chrysogaster) is Australia's largest rodent. -
Chuck Noblet asked the new improved ChatGPT5 to generate a map of the US with all the states named.Chuck Noblet asked the new improved ChatGPT5 to generate a map of the US with all the states named. It's best to look at it starting from the west and then going east.
Chuck Noblet (@chucknoblet.bsky.social)
"generate a map of the USA with each state named"
Bluesky Social (bsky.app)
-
Here's a simple-sounding unsolved problem:Here's a simple-sounding unsolved problem:
Starting with the number 8, and repeatedly adding half of the number to itself, rounding down to get a whole number, will there eventually be a point where you have seen more than twice as many odd numbers as even numbers? The sequence starts like this:
8 → 12 → 18 → 27 → 40 → 60 → 90 → 135 → 202 → …
The answer is probably 'no', but settling this question will help people find a better lower bound on BB(6), the 6th busy beaver number. This is the largest number of steps it takes for a 6-state Turing machine to halt, among those that actually halt.
The function BB is uncomputable, in general, but people have computed BB(1), BB(2), BB(3), BB(4) and BB(5). So, we know
BB(5) = 47,176,870
But BB(6) is a lot bigger! Since June we've known
BB(6) ≥ 2 ↑↑ (2 ↑↑ (2 ↑↑ (2 ↑↑ 2)))
What the hell does that mean? Well, this ↑↑ thing works like this: 2 ↑↑ 2 is just 2^2, and 2 ↑↑ 3 = 2^(2^2), and so on. So
2 ↑↑ (2 ↑↑ 2) = 2 ↑↑ 4 = 2^(2^(2^2)) = 2^(2^4) = 2^16 = 65536
so 2 ↑↑ (2 ↑↑ (2 ↑↑ 2)) is 2 raised to itself 2^65536 times, and then 2 ↑↑ (2 ↑↑ (2 ↑↑ (2 ↑↑ 2))) is 2 raised to itself *that* meany times.
So BB(6) is quite big. But nobody knows how big... because there are lots of 6-state Turing machines that experts are still scratching their heads over. Figuring out which ones halt requires solving some hard math problems, including the one I mentioned at the start.
This problem has a name: it's called the Antihydra problem. You can learn more about it here:
Working on this isn't very useful. But it's fairly harmless, unlike what most rich people do for fun, and if you solve it you'll win this plaque:
